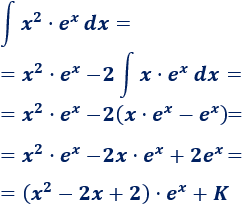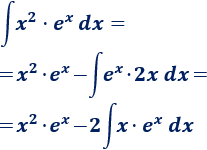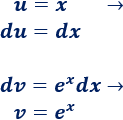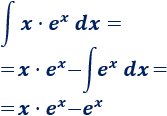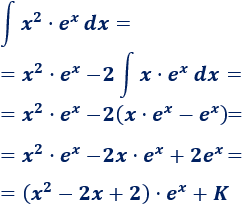Cálculo Integrales

                  Cálculo Integral 

                     (integrales)

El cálculo integral, encuadrado en elcálculo infinitesimal, es una rama de las matemáticas en el proceso de integración o antiderivación. Es muy común en la ingeniería y en la ciencia; se utiliza principalmente para el cálculode áreas y volúmenes de regiones y sólidos de revolución.

Función: se obtiene por una operación a partir de la derivada.

"el problema consiste en hallar la integral de la función dada.

        Integrales               definidas

 te voy a explicar qué es una integral definida y cómo se calcula.

Integral definida. Dada una función  f(x) y un intervalo [a,b], lDada la integral definida es igual al área limitada entre la gráfica de f(x), el eje de abscisas, y las rectas verticales x = a y x = b.

Ejemplo

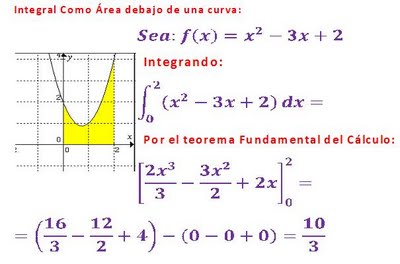La imagen de ejemplo tiene un error en el primer término, al integrar x^2 queda x^3/3, luego al remplazar 2 en x, queda 8/3, siendo el resultado 2/3

Aplicaciones

El concepto de integral tuvo su origen histórico de el área la necesidad de resolver problemas concretos como: cálculo de área  limitada por dos curvas,longitudes de arcos, volúmenes,trabajo, velocidad, momentos de inercia, etc.; todos estos cálculos se pueden realizar mediante la integral definida.
Integral indefinida
Es el conjunto de las infinitas primitivas que puede tener una función.

Una primitiva de la función ${\displaystyle \scriptstyle f(x)=\cos(x)}$en ${\displaystyle \scriptstyle \mathbb {R} ,}$ es la función ${\displaystyle \scriptstyle F(x)=\sin(x)}$ ya que:

Dado que la derivada de una constante es cero, tendremos que cos(x) tendrá un número infinito de primitivas tales comosin(x), sin(x) + 5, sin(x) - 100, etc. Es más, cualquier primitiva de la funciónf(x) = cos(x) será de la forma sin(x) + Cdonde C es una constante conocida cómo constante de integración.
Tutorial(Video):
https://youtu.be/Fj8SHHJIElU

Integrales inmediatas

¿Qué son las integrales inmediatas?

Son integrales que se resuelven de una forma directa, aplicando su fórmula correspondiente. Para poder aplicar el método de integrales inmediatas, hay que transformar la función a integrar, mediante las propiedades de las integrales, para que quede de la misma forma que figura en cada una de las fórmulas.

Ejercicio

(Ejemplo)

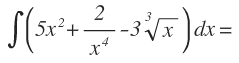
En primer lugar separamos cada término de la función en una nueva integral, aplicando una de las propiedades de las integrales:

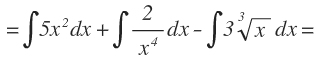
Ahora en cada integral, sacamos fuera las constantes:

Cada una de las integrales que nos ha quedado, aunque no lo parezca, se resuelven con la integral inmediata de la función potencial simple, ya que las funciones son de la forma de x elevada a un número:

A la primera integral no hay que hacerle nada, pero a la segunda y la tercera integral, debemos transformarlas para que estén de la misma manera. En la segunda integral, subimos la potencia al numerador y le cambiamos el signo y en la tercera, ponemos la raíz en su forma exponencial:

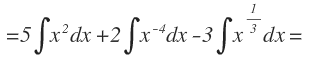
Ahora ya podemos aplicar la fórmula de la integral inmediata en cada una de las integrales:

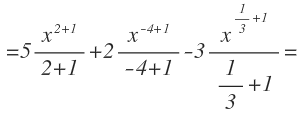
Ya hemos integrado. Ahora vamos operar. Realizamos las sumas que nos han quedado en los exponentes y denominadores:

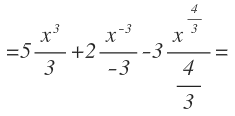
Y finalmente multiplicamos los números que nos han quedado, dejamos todos los exponentes como positivos o los volvemos a pasar a raíz y le añadimos la constante:

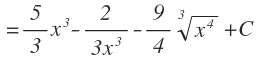
lista de integrales inmediatas

Ejemplo

Calculamos la integral

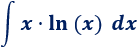
El integrando es un producto de dos funciones.

1. Identificamos $u$ y $dv$

Es importante pensar la elección de $u$ y $dv$ porque luego tenemos que derivar $u$ e integrar $dv$. Además, tenemos que calcular la integral de la fórmula.

Si escogemos $u=x$, entonces su derivada es $du=dx$. Pero, entonces, tenemos que escoger $dv=ln\left(x\right)dx$ y para calcular $v$ tenemos que integrar el logaritmo.

Por tanto, escogemos la otra opción:

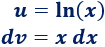
2. Calculamos $du$ y $v$

Para calcular $du$ tenemos que derivar $u$:

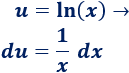
Para calcular $v$ tenemos que integrar $dv$:

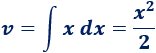
3. Aplicamos la fórmula

Sólo tenemos que sustituir las variables de la fórmula:

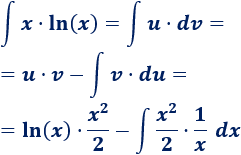
4. Calculamos la integral que queda

La integral que queda es inmediata:

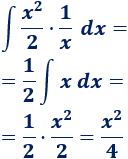
Por tanto,

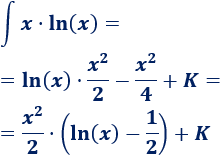
No olvidéis la constante de integración $K$.

Más integrales resueltas

No es necesario tener un producto en el integrando para aplicar integración por partes. La siguiente integral es un ejemplo de ello.

 Integral 1

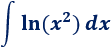
Antes que nada, aprovechamos las propiedades de los logaritmos para simplificar el integrando:

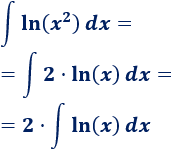Vamos a calcular la integral del logaritmo natural (luego ya multilicaremos por 2).
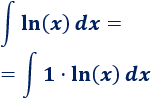
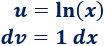
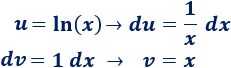
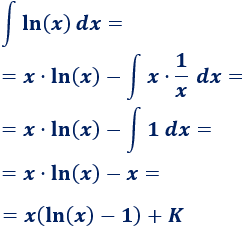
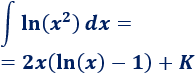
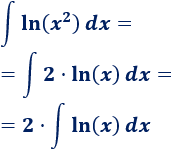
Podemos escribir el integrando como un producto para ver claramente la aplicación de la fórmula:

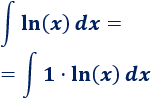
1. Identificamos $u$ y $dv$

Obviamente, no debemos escoger $dv=ln\left(x\right)dx$ ya que entonces, tendríamos que calcular la integral del logaritmo, que es precisamente lo que estamos haciendo. Por tanto,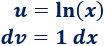

2. Calculamos $du$ y $v$

Derivamos e integramos: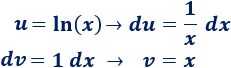

3. Aplicamos la fórmula

Sustituimos en la fórmula: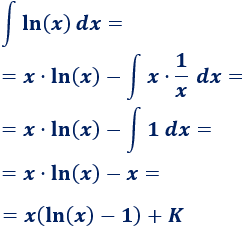

Por tanto, la integral del problema es

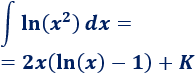
En algunas integrales tendremos que aplicar el método varias veces. En estos casos, es importante mantener la elección de los factores $u$ y $dv$. La siguiente integral es un ejemplo de ello.

Integral 2

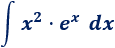El integrando es un producto de dos funciones.

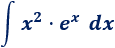
1. Identificamos $u$ y $dv$

No importa si $e^x$ es $u$ ó $dv$ porque tanto su derivada como su integral es $e^x$.
Si escogemos $dv=x^2$, tendremos que calcular la integral

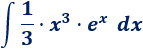Así que es mejor escoger $u=x^2$ para bajar el grado del monomio.

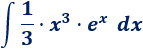
2. Calculamos $du$ y $v$

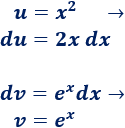
3. Aplicamos la fórmula

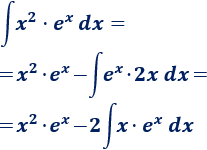Aplicamos de nuevo integración por partes para calcular la integral que nos queda. Para no deshacer los cálculos anteriores, mantenemos la elección de $u$ y $dv$:

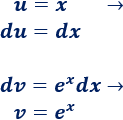Por tanto,

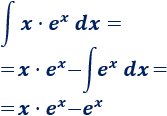Volviendo al comienzo,